[GameMath] 벡터
들어가며
이번 시간에는 C++ STL의 std::vector처럼 데이터를 저장하는 컨테이너가 아니라, 수학적으로 크기와 방향을 가지는 기하 벡터의 개념과 게임에서의 활용을 알아본다.
벡터
스칼라 vs 벡터
- 스칼라: 하나의 숫자 값
- 벡터: 크기(magnitude)와 방향(direction)을 가진 값
예시
- A에서 B까지의 거리가 5일 때,
- 스칼라: 거리 5 (어디든 5 떨어진 지점)
- 벡터: A에서 B를 정확히 가리키는 방향 + 거리
벡터 개념
- 벡터 개념
- 기하 벡터: 수학적 벡터 (방향 + 크기)
- 위치 벡터: 좌표를 표현하는 벡터 (게임 오브젝트의 위치 등)
- 벡터의 표현
- 목적지 좌표에서 시작지 좌표를 빼는 방식으로 표현한다.
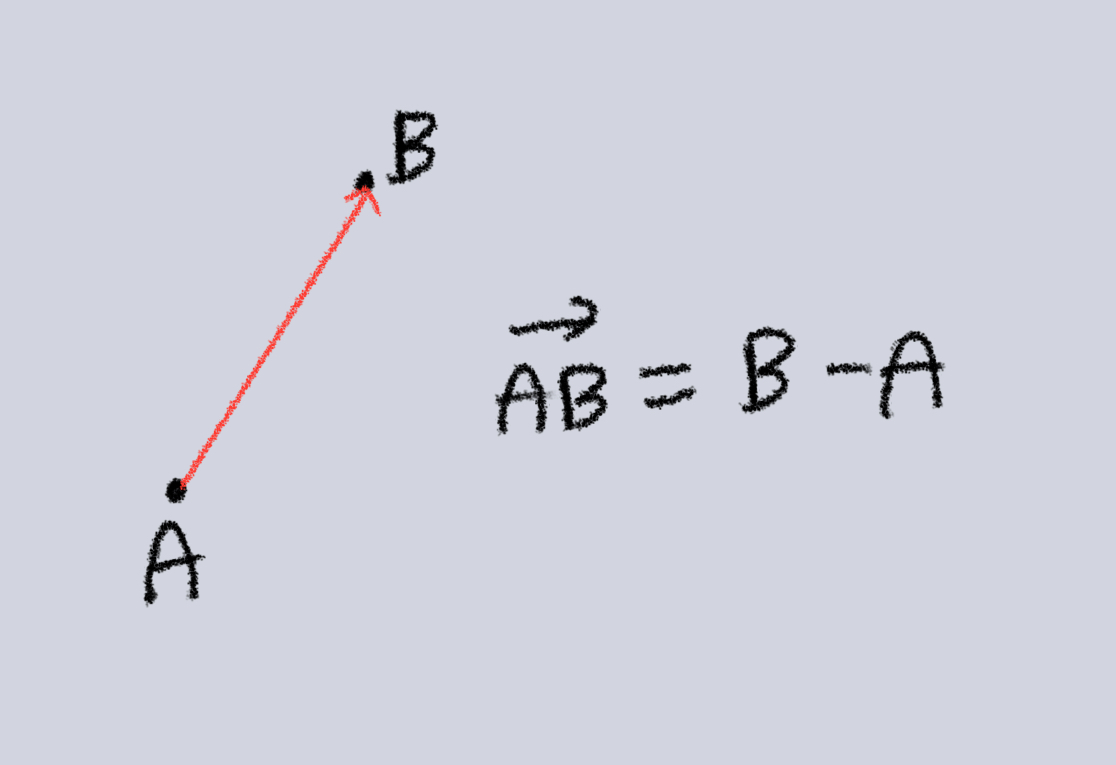
- 목적지 좌표에서 시작지 좌표를 빼는 방식으로 표현한다.
- 벡터의 성질
- 벡터와 벡터의 곱셈/나눗셈은 정의되지 않는다.
- 벡터와 벡터의 곱셈/나눗셈은 정의되지 않는다.
-
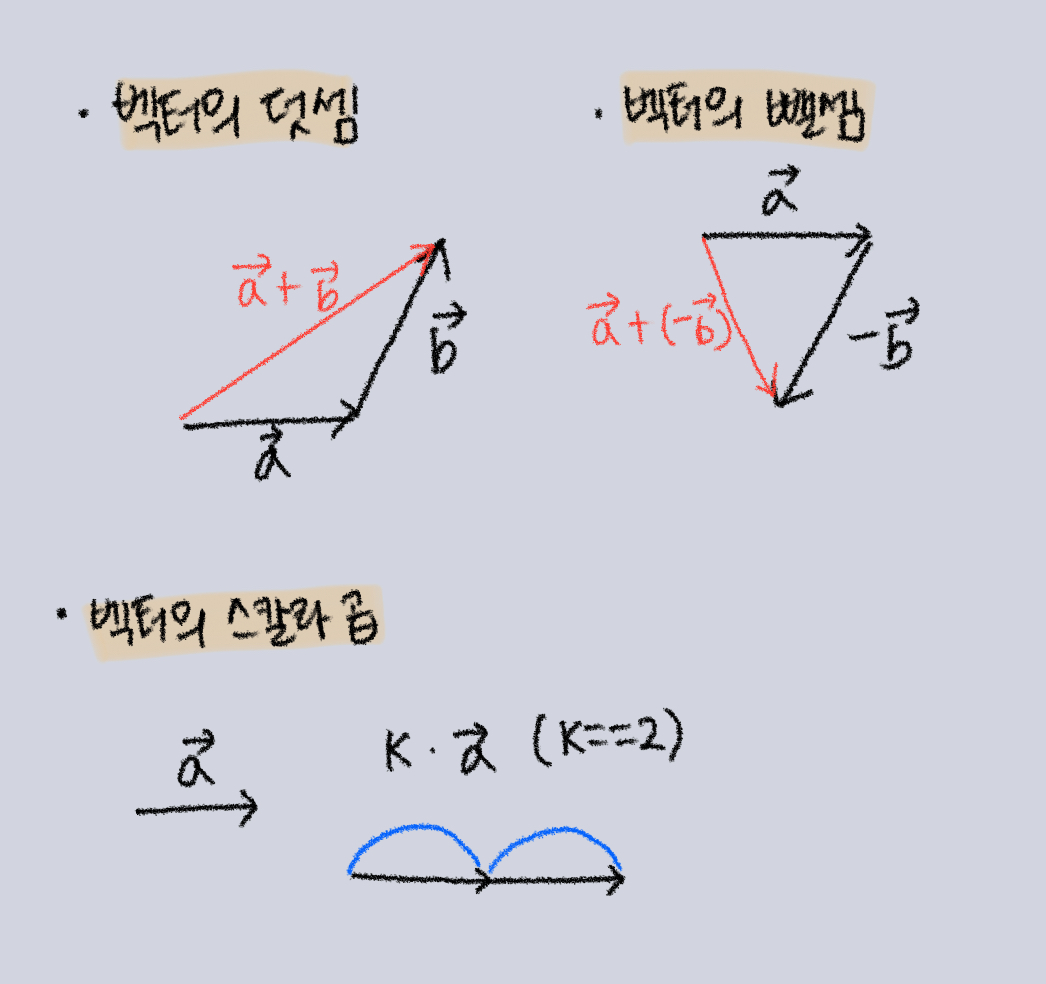
벡터의 연산법칙

- 벡터의 크기와 단위 벡터
- 단위 벡터: 크기가 1인 벡터로 방향만 유지하고 크기를 제거한다.

- 단위 벡터: 크기가 1인 벡터로 방향만 유지하고 크기를 제거한다.
활용 예시
- 방향을 구한 후
속도 * 시간을 곱해 이동 계산
magnitude(): 벡터의 크기를 구하는 함수normalize(): 단위 벡터를 구하는 함수
내적
-
공식

-
특징
- 교환법칙이 성립
- 결과는 스칼라
활용 예시
- 두 벡터의 방향 차이를 구해 각도 비교, 데미지 계산
- 아크 코사인(acos) 대신 간단한 내적 계산을 통해 성능 최적화 가능
dot()함수 사용
외적
-
공식
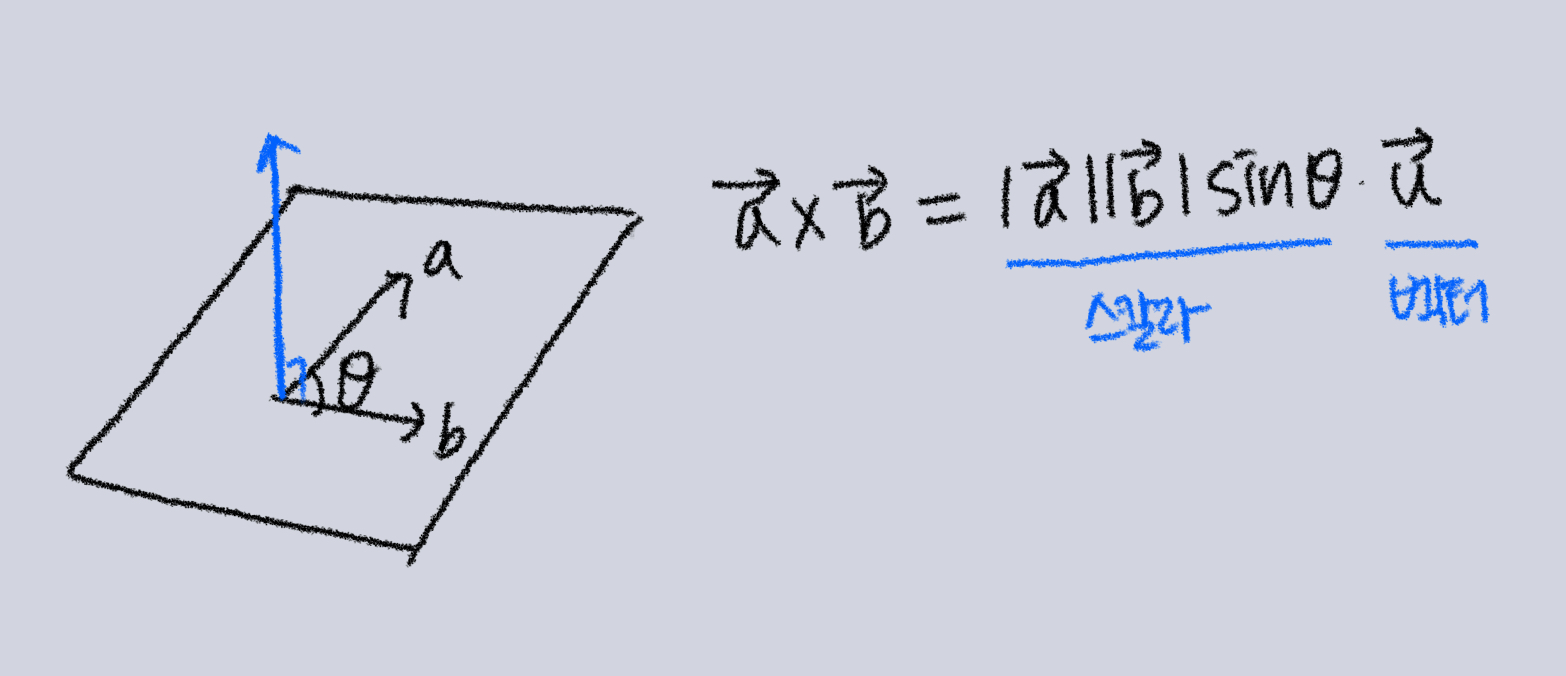
-
특징
- 교환 법칙이 성립하지 않음 - 방향이 반대
- 결과는 수직 벡터 (벡터 값)
활용 예시
- 법선 벡터 구하기
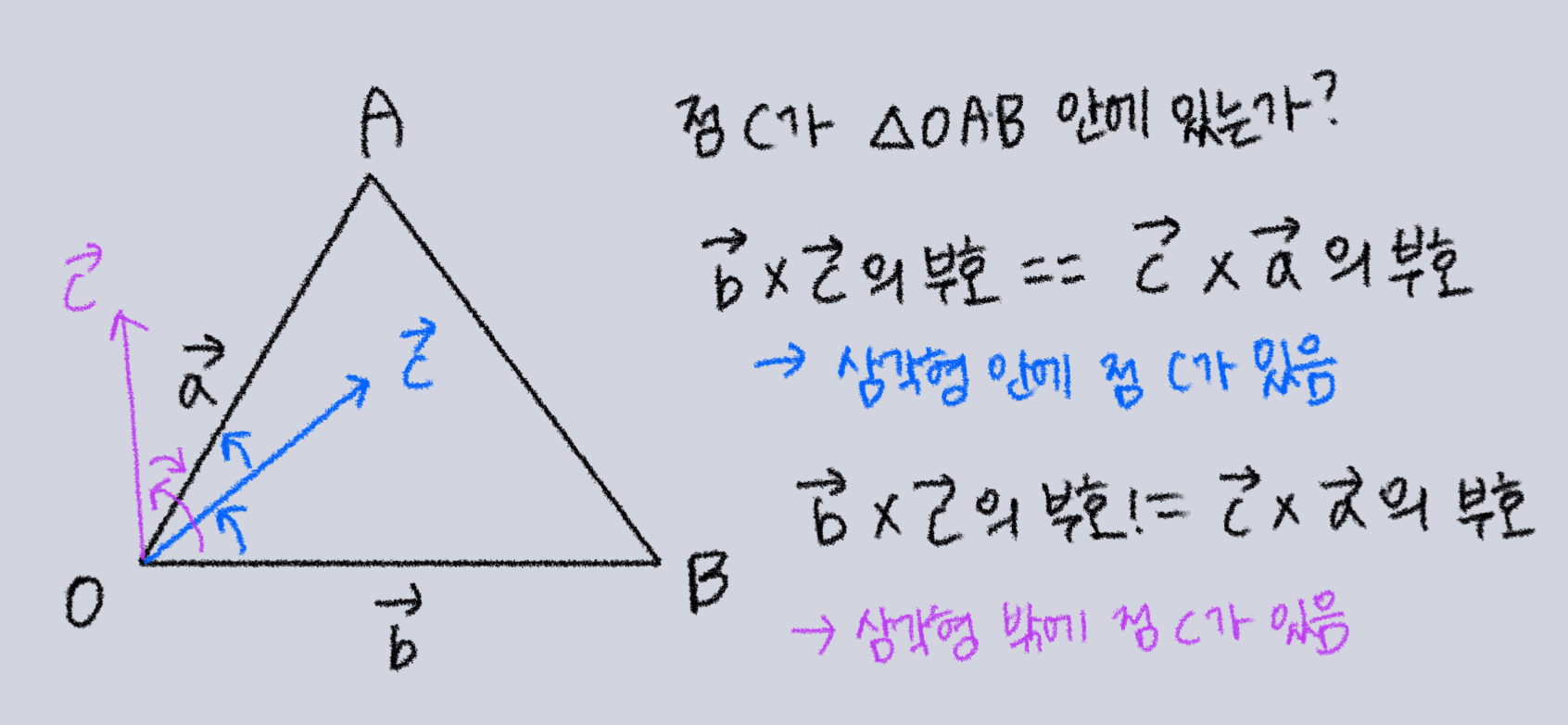
- 삼각형 안에 점이 존재하는지 판별 (삼각형 OAB 안에 점 C가 존재하는지?)
- 쿨타임 UI 색칠 여부 계산
cross()함수 사용
마치며
삼각함수에 이어 벡터도 복습했는데 벡터의 내적과 외적이 게임에서 어떻게 활용되는지를 이해하는 게 가장 중요한 것 같다. 잊을만하면 복습하도록!!

Leave a comment