[GameMath] Scale, Rotation, Translation
들어가며
이번 시간에는 행렬을 이용한 연산 세 가지 Translation(평행이동), Scale(크기 변경), Rotation(화전)를 알아본다.
Translation
게임에서 객체의 위치를 이동시키는 걸 Translation이라고 한다.
-
(x, y, z)좌표를(a, b, c)만큼을 이동시키고 싶을 때, 3차원 벡터로는 이동 행렬을 곱셈으로 처리하기 어렵다.
-
따라서
w성분을 1로 사용하면 4x4 행렬 곱을 통해 좌표에 일정 값을 더하는 이동 변환을 적용할 수 있다.- 이를 동차 좌표계라고 하는데, 동차 좌표계는 n차원의 좌표를 n+1개의 요소로 표현한다.
- 동차 좌표계는 기존 좌표 (x, y, z)를 (x, y, z, 1)로 표현한다.

Scale
객체의 크기를 키우거나 줄이는 작업을 Scale이라고 한다. 각 축에 대해 독립적인 비율로 크기를 조정할 수 있다.
(x, y, z)에 대해 각a, b, c만큼의 크기 조절을 적용해보자.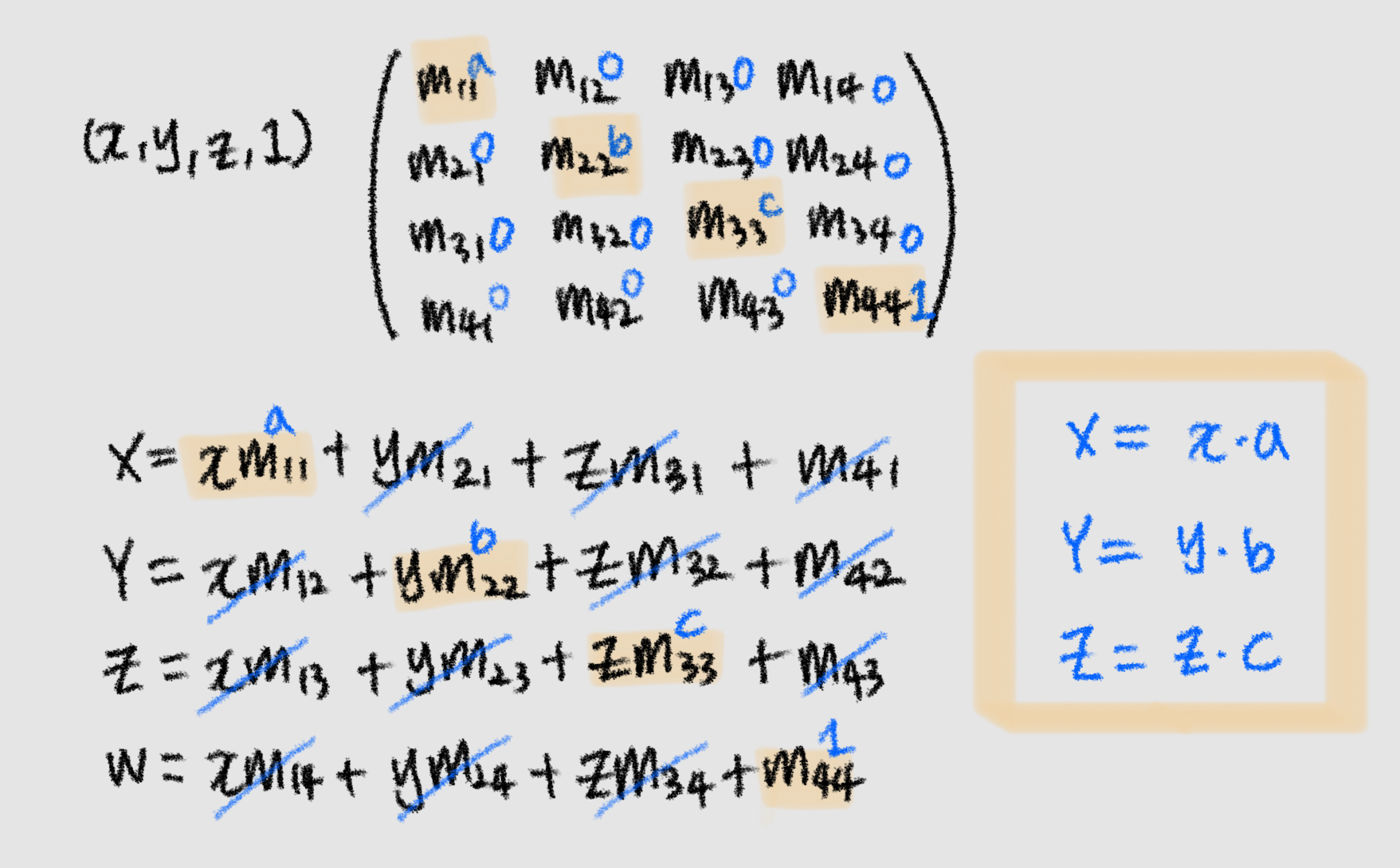
- 주의할 점
- 원점을 기준으로 Scale 연산을 적용하지 않으면 객체가 왜곡되거나 엉뚱한 방향으로 커질 수 있다.
- 참고. 게임에서는 대개 플레이어의 발을 기준으로 좌표를 세팅한다.
Rotation
회전은 앞의 변환보다 더 까다로운 변환이다. 예를 들어 z축을 기준으로 회전하면 (x, y) 평면에서 원형으로 회전하게 된다.
- 회전은 특정 축을 중심으로 이루어지고, 삼각함수의 개념이 사용된다.
- 점 A에서 B로 세타만큼 회전시켜보자.
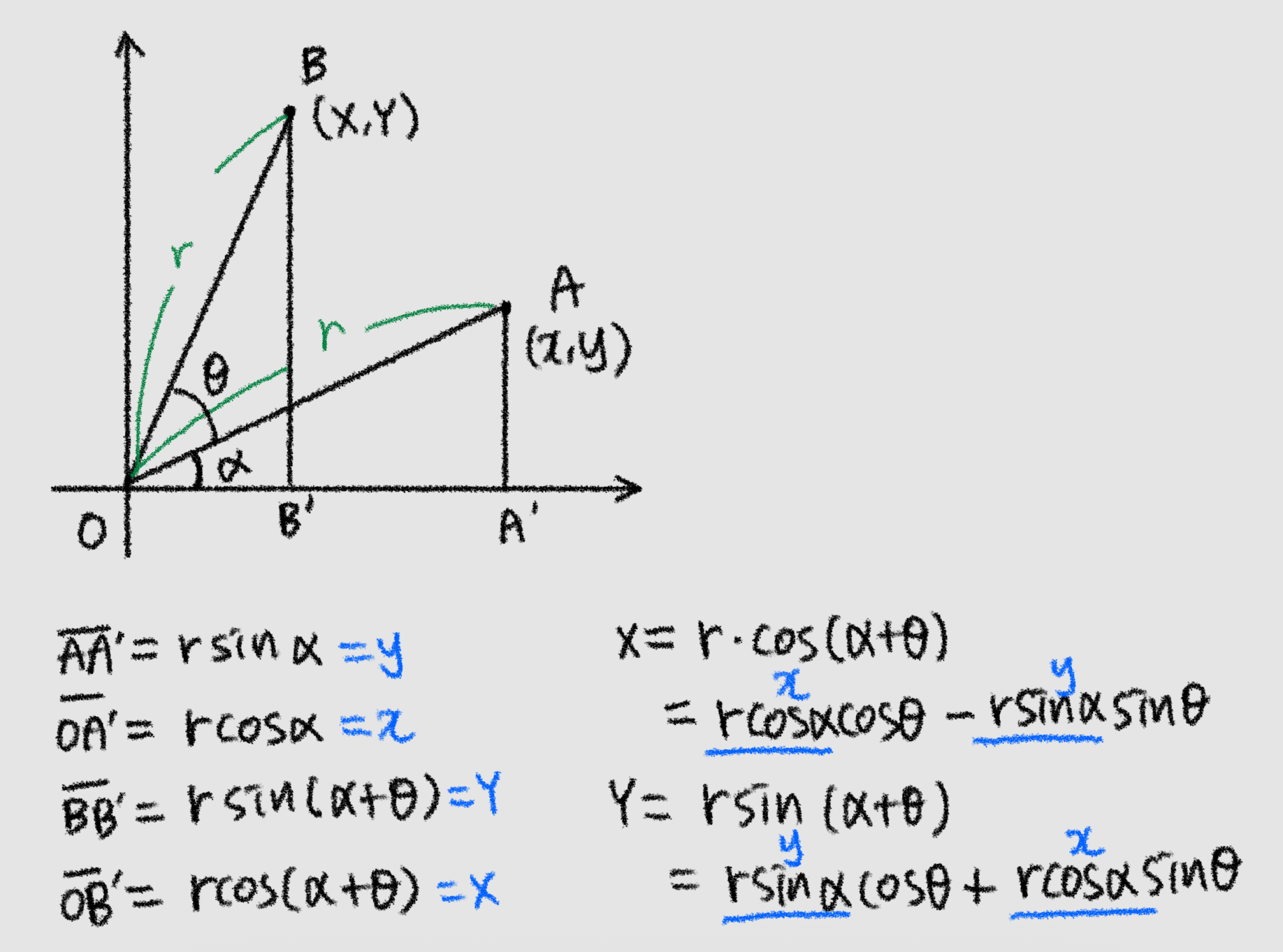
- 행렬로 나타내면 다음과 같다.
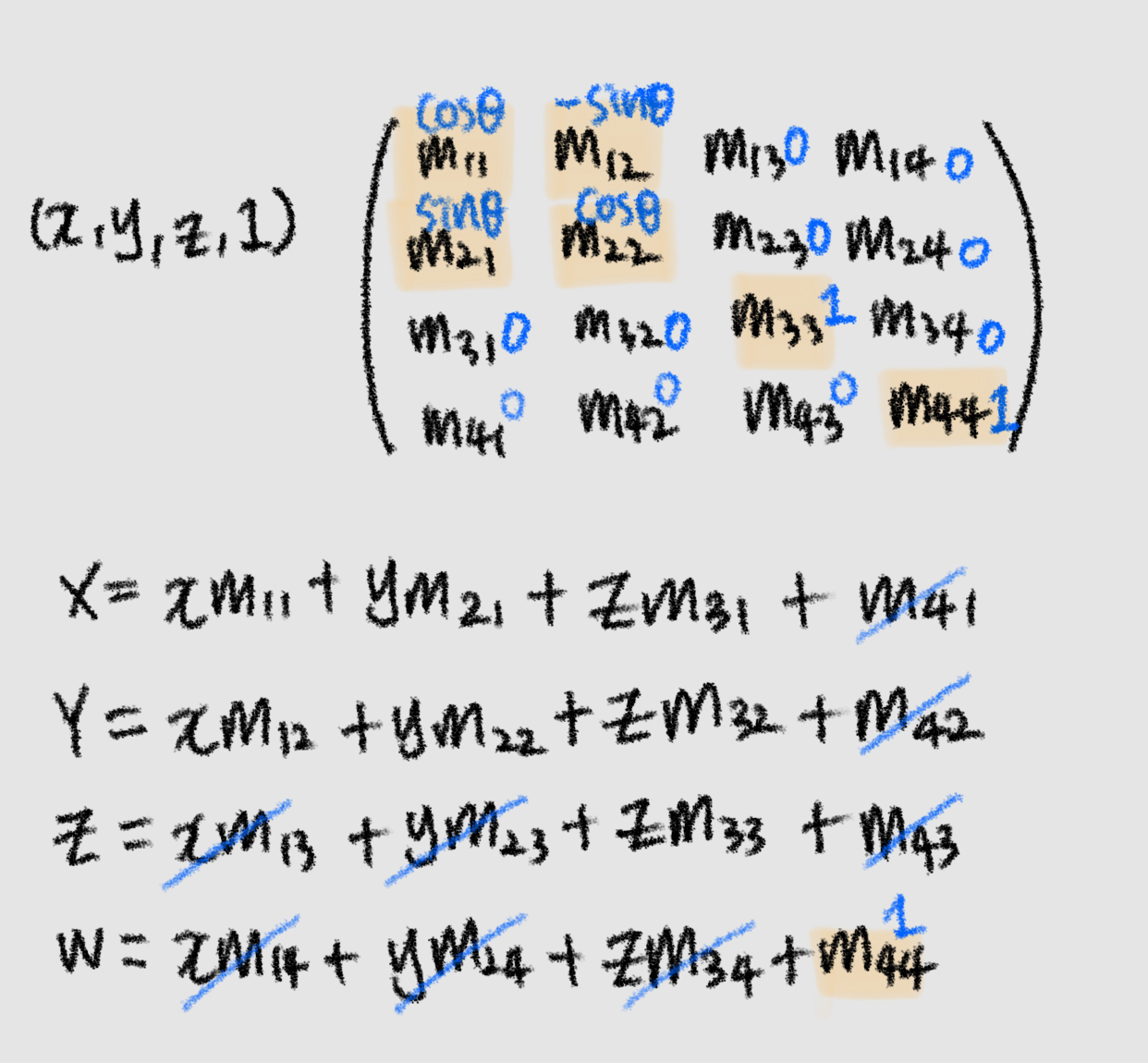
- 점 A에서 B로 세타만큼 회전시켜보자.
- 자전 vs 공전
- 자전: 자신의 축을 중심으로 도는 회전으로, 지구가 자전하는 개념과 같다.
- 공전: 외부의 기준점을 중심으로 도는 회전으로, 지구가 태양을 공전하는 개념과 같다.
- 게임에서는 대부분 자전을 주로 사용한다.
연산 순서
- 행렬의 곱은 교환법칙이 성립하지 않지만(
A * B ≠ B * A), 결합법칙은 성립한다((A * B) * C = A * (B * C)). - 반드시 SRT 순서로 연산해야 한다.
- 순서가 바뀌면?
- Translation → Rotation: 공전이 된다.
- 순서가 바뀌면?
마치며
이번 시간에는 행렬로 Scale, Rotation, Translation을 계산하는 방법에 대해 알아봤다. 결합법칙을 이용해서 세 가지 연산을 하나의 행렬로 담는다는 게 정말 대단한 것 같다. 이런 개념을 게임에 적용한 것도 신기하다. 행렬이 있기에 게임 내부 연산이 빠르게 돌아가는 거겠지!?

Leave a comment